2.1 인공 뉴런: 초기 머신 러닝의 간단한 역사
- 퍼셉트론(Perceptron)
프랑크 로젠블라트가 MCP(맥컬록-피츠) 뉴런 모델을 기반으로 퍼셉트론 학습 개념을 처음 발표했다. 그는 퍼셉트론 규칙에서 자동으로 최적의 가중치를 학습하는 알고리즘을 제안했다. 이 알고리즘 샘플로 한 클래스에 속하는지 아닌지를 예측 가능하다.
- 인공 뉴런의 수학적 정의
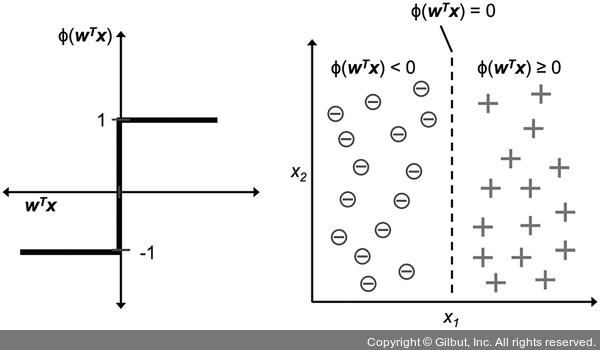
인공 뉴런의 아이디어를 두 개의 클래스가 있는 이진 분류 작업으로 볼 수 있다. 두 개의 클래스는 양성(1)과 음성(-1)으로 나타낸다. 그 후 입력 값 x와 이에 상응하는 가중치 벡터 w의 선형 조합으로 결정 함수(ϕ(z))를 정의한다. 이에 따른 최종 입력인 z는 z = w1x1+...+wmxm이다. 이제 x의 최종 입력이 사전에 정의된 임계 값 θ보다 크면 클래스 1로 예측하고,그렇지 않으면 클래스 -1로 예측한다.
임계 값 θ를 식의 왼쪽으로 옮겨 w0 = -θ이고 x0 = 1인 0번째 가중치를 정의한다.
z = w0x0 + w1x1 + ... + wmxm = wTx
머신 러닝 분야에서 w0 = -θ을 절편이라고 한다.
- 퍼셉트론 학습 규칙
- 가중치를 0 또는 랜덤한 작은 값으로 초기화한다.
- 각 훈련 샘플 x에서 다음 작업을 한다.
- 출력 값 y를 계산한다
- 가중치를 업데이트한다
2.2 파이썬으로 퍼셉트론 학습 알고리즘 구현
- 객체 지향 퍼셉트론 API
Perceptron 객체를 초기화한 후 fit 메서드로 데이터에서 학습하고, 별도의 predict 메서드로 예측을 만든다.
- 퍼셉트론 구현 법
import numpy as np
class Perceptron(object):
"""퍼셉트론 분류기
매개변수
-------------
eta : float
학습률 (0.0과 1.0 사이)
n_iter : int
훈련 데이터셋 반복 횟수
random_state : int
가중치 무작위 초기화를 위한 난수 생성기 시드
속성
-------------
w_ : 1d-array
학습된 가중치
errors_ : list
에포크마다 누적된 분류 오류
"""
def __init__(self, ata=0.01, n_iter=50, random_state=1):
self.eta = eta
self.n_iter = n_iter
self.random_state = random_state
def fit(self, X, y):
"""훈련 데이터 학습
매개변수
----------
X : {array-like}, shape = [n_samples, n_features]
n_samples개의 샘플과 n_features개의 특성으로 이루어진 훈현 데이터
y : array_like, shape = [n_samples]
타깃 값
반환 값
---------
self : object
"""
rgen = np.random.RandomState(self.random_state)
self.w_ = rgen.normal(loc=0.0,scale=0.01,size=1 + X.shape[1])
self.errors_ = []
for _ in range(self.n_iter):
errors = 0
for xi, target in zip(X, y):
update = self.eta * (target - self.predict(xi))
self.w_[1:] += update * xi
self.w_[0] += update
errors += int(update != 0.0)
self.errors_.append(errors)
return self
def net_input(self, X):
"""최종 입력 계산"""
return np.dot(X, self.w_[1:}] + self.w_[0])
def predict(self, X):
"""단위 계단 함수를 사용하여 클래스 레이블을 반환합니다"""
return np.where(self.net_input(X) >= 0.0, 1, -1)
- eta와 에포크 횟수(훈련 데이터를 반복하는 횟수) n_iter로 새로운 perceptron 객체를 초기화 한다.
- self.w_[0]은 절편
- rgen.normal을 사용하여 표준편차가 0.01인 정규 분포에서 뽑은 랜덤한 작은 수 포함
- 가중치가 0이 아닌 이휴는 eta가 분류 결과에 영향을 주기 때문
- fit 매서드는 가중치를 초기화한 후 훈련 세트에 있는 모든 개개의 샘플을 반복 순회하면서 이전 절에서 설명한 퍼셉트론 학습 규칙에 따라 가중치를 업데이트한다.
- 가중치를 업데이트하기 위해 predict 매서드를 호출해서 클래스 레이블에 대한 예측
- predict 매서드는 모델이 학습된 후, 새로운 데이터의 클래스 레이블을 예측하는 데도 사용 가능
- 에포크마다 self.errors_ 리스트에 잘못 분류된 횟수를 기록.
- net_input 메서드에서 사용한 np.dot 함수는 벡터 점곱 wTx를 계산한다.
- 붓꽃 데이터셋에서 퍼셉트론 훈련
- 붓꽃 데이터셋 산점도 그리기
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
df = pd.read_csv('https://archive.ics.uci.edu/ml/''machine-learning-databases/iris/iris.data',
header=None)
print(df.tail())
# setosa와 versicolor를 선택한다
y = df.iloc[0:100, 4].values
y = np.where(y == 'Iris-setosa', -1, 1)
# 꽃받침 길이와 꽃잎 길이를 추출한다.
X = df.iloc[0:100,[0,2]].values
# 산점도를 그린다.
plt.scatter(X[:50,0], X[:50,1],
color ='red', marker = 'o', label = 'setosa')
plt.scatter(X[50:100,0], X[50:100,1],
color ='blue', marker = 'x', label = 'versicolor')
plt.xlabel('sepal length [cm]')
plt.ylabel('petal length [cm]')
plt.legend(loc='upper left')
plt.show()

- 퍼셉트론의 에포크 대비 오차 확인하기
ppn = Perceptron(eta=0.1, n_iter=10)
ppn.fit(X, y)
plt.plot(range(1, len(ppn.errors_) + 1), ppn.errors_, marker='o')
plt.xlabel('Epochs')
plt.ylabel('Number of errors')
plt.show()

반응형
'Study > ML&DL' 카테고리의 다른 글
| 10. 회귀 분석으로 연속적 타깃 변수 예측 (0) | 2020.03.17 |
|---|---|
| 8. 감성분석에 머신 러닝 적용 (0) | 2020.03.03 |
| 6. 모델 평가와 하이퍼파라미터 튜닝 (0) | 2020.02.18 |
| 5. 차원 축소를 사용한 데이터 압축 (0) | 2020.02.10 |
| 1. 컴퓨터는 데이터에서 배운다. (0) | 2020.01.11 |




댓글